| Issues of the Questaholic Magazine | March 2023 |
Table of Contents
- An Interview With Pyat by Xurdones
- The OSRS Farming Guild by Francine1225 and Diapolo10
- The Clan Quest Test Kitchen: Chicken Noodle Soup by Darkestnight
- The...Christmas Tree Variation? by Derparnieux
- Shiro Applies Maths: Music Theory - The Final Note by Shiro Shana
- Xurdones Reviews: Glass Onion (2022) by Xurdones
Letter From Your Editor
Well folks, this is it: the last Questaholic of 2022. It's a bit of a tough act to follow Cireon's incredible Advent Calendar event (over $1200 raised for St. Jude Children's Research Hospital!), but I couldn't be more proud of what the team has put together, and I hope you enjoy it!
If you'll allow me to get mushy for a second, when I started working on the magazine in February, I wasn't sure how it would go; four issues later, I still don't know how it's going to go, but it's been a great ride getting here. It hasn't always been easy, and I've made some mistakes I hope to learn from in the coming year, but it's also been a lot of fun, and it means a lot to be able to put this rag out into the world every couple of months. So I'd like to extend an extra-special thank you to Choto, for your confidence in pushing me to take on this role; I couldn't have done it without you.
And, of course, this entire venture would have fallen flat without our wonderful production team, so let me extend a heartfelt "thank you" to everyone who contributed to the magazine this year: Choto, Cyan Ryder, Darkestnight, Derp, Diapolo10, Francine, Miss Alaska, Questcaping, Shane, Shiro, and Tyco; and a second, equally massive thanks to Questcaping, for lending his time and abilities to creating the covers for each issue.
And, even more "of course", a huge thanks to everyone who agreed to be interviewed for the magazine this year: Darkestnight, Duke Juker, Uptheirons05, and our newest interviewee Pyat. Interviews with Clannies is far and away my favourite part of the magazine (unless you're an article writer, then my favourite is your column, honest!); I love that we can shine a spotlight on the amazing community we've built up, and tell a story for every member.
I'll end of this note with my usual calls to action: if anyone reading this would be interested in contributing to a future issue, either on a one-off basis or as a recurring feature, please don't hesitate to reach out to me on Discord or send me a private message on the offsite. I'd love to have you! And, likewise, if you have any feedback on this issue or the magazine generally - anything you'd like to see more of, or less of, or something that isn't here that you'd like to see - my dms are always open.
With that, on behalf of the entire Questaholic team I'd like to wish you a very happy 2023. Enjoy the magazine, and we'll see you again in the spring!
Article by Xurdones
QUESTAHOLIC PRESENTS
An interview with Pyat
He's the one on the right
by Xurdones.
<::::::::::::::::::::::::::::::::::}]xxxx()oGENERAL
What are you currently studying?
I’m learning to be a Software Developer.
What do you do for a living?
I currently work in a supermarket, but want to change career.
Reason is to have a future.
Been working in retail for 4+ years without any growth, time to choose for myself and my ambitions.
What's your favourite sport?
Skateboarding no doubt.
It’s super technical and really impressive.
I don’t skate as much as I’d like anymore with my life being as busy as it is, but I still enjoy it from time to time.
Not a great skater, but just rolling around, it’s cosy.
Which are your favourite childhood cartoons?
Dexter’s Laboratory, Cow ‘n Chicken, Ren and Stimpy.
Basically Cartoon Network junk.
My wife didn’t enjoy any of those shows.
If you could have any super power other than invincibility, what would you choose and why?
Strong and nimble, like a Saiyan from Dragonball Z.
Ability to fly, etc.
What are your favourite outdoor activities?
Skateboarding, walking in nature.
Which is your favourite movie?
Tough one. I like a lot.
One of my favourites is Starship Troopers, though.
Also Dragonball Super: Super Hero is a great film as well.
What sort of music and artists do you listen to?
I listen to a varied range of music.
But often enough I come back to Eurobeat.
If you don’t know of it here’s a good link about it:
Which books would you recommend?
I don’t really read books. :(
What's your favourite type of food?
I once made a spicy mango curry with rice, it was so good.
But generally I really enjoy asian dishes.
Indian curries are really nice too.
I can never make a sauce as good as they can, though.
Do you prefer mom's food or restaurant food?
Restaurant food.
I love dining out, can be expensive at times, but very worth it.
(I like my whiskeys and liquor)
GAMING
Which are your favourite games?
The World Ends With You on the DS.
That’s one of the most inspirational games I ever played.
Life-changing in a sense. (When I was 15/16)
Also Runescape.
What are your favourite video game genres?
Ones that have a good or fun story.
Also Skateboarding games.
Did you know I was a renowned speedrunner in Tony Hawk games?
A fellow speedrunner made a small doc about me!
Which was the most difficult video game you ever beat?
Tough one, I think Demon’s Souls on the PS3?
I’m not great with games too much.
What's the toughest thing you've ever accomplished in a video game?
Beating Ninja Gaiden on the NES.
Took me a while and yes, frustration was had.
When playing with friends, do you prefer video games or tabletop games, and why do you prefer one over the other?
Either is fine, as long as you have fun.
RUNESCAPE
What's your favourite skill?
Runecrafting.
The whole idea of needing/providing runes, being able to craft them and use them for Magic, is really neat.
Just like smithing bars for armour.
Being all self-sufficient is really awesome in my opinion.
But I will never make an iron-man.
What's your favourite quest?
Evil Dave’s Big Day Out.
When did you start playing?
My character isn’t that old as I started over fresh to ease myself back into Runescape.
But I started when I was like 2005 or 2006 I think.. I can’t recall, really.
What was your very first accomplishment?
My proudest moment was when I was young, mining hard for someone else, delivering them coal for gp. When I could enter the Mining Guild I was ecstatic.
Odd nowadays, but it was the coolest thing in my eyes to be able to use the ladders down in Falador.
You get 30 seconds of full attention from all employees of Jagex. What do you say?
Priff was a mistake and it locks out lower leveled players away from high leveled players.
It’s more fun to be all mixed.
Now with 2 (Basically 3 grand exchanges) you barely see another player.
You get a ticket to visit Gielinor IRL. Where do you go first?
Varrock, always been the coolest town in my eyes.
Which is the most interesting God? Why?
Brassica Prime, because he’s just the most fun. Deliciousness be with you.
GENERAL PART 2
What are your biggest dreams in life?
To be able to pick my own path in life.
Which I’m currently striving to do.
If you could have any 3 animals in the world (only real animals, not fictional), which would you pick?
Cat, cat, cat.
If you had to give up one of your senses (sight, hearing, touch, smell, taste) which one would you pick?
Smell.
If I can still taste, I don’t mind losing my smell.
How would you describe yourself to others?
Introverted idiot that only got his life together at 31.
(My wife says I talk myself down a lot)
Other than that,
What is your most used item in your daily life?
My pen.
I take too many old-school paper notes about anything.
If I were to visit your country, what do you think I should do first?
Check out the Dom tower in Utrecht.
What are your favourite cities/locations, both in RS and in real life?
RS:
- Varrock, Falador
Real life:
Anything out in nature, I love walks in forests and such.
Do you have a motto or a favourite phrase? If so, which is it?
Strangely it comes from the Wiccan Rede:
When ye have a true need, hearken not to others' greed.
It basically means it’s okay to be selfish every now and then.
That it’s okay to put yourself first instead of others.
Something I never used to do, myself.
Hence why I think lowly of myself, but my wife’s helping me to get me out of that mind-set.
Do you play an instrument? If not, which instrument/s would you like to learn?
None, I really like bass-guitar.
Tell us the story behind your name!
Pyat - it’s short for Pyatters.
It’s derived from a person’s online username I once liked when I was young called Nyanners.
And my name being Patrick, I went for Pyatters - And in short Pyat.
I was lucky Pyat was available in-game!
It also means 5 in Russian, apparently.
How many languages do you speak? Which one would you like to learn?
Dutch, English, so basically 2.
Not really too interested in other languages, to be honest.
If you had to escape your country immediately, what's the one thing you'd take with you?
Phone - to be able to pay for a charger using my mobile paying, be able to call my wife and kid, stuff like that.
What's your first memory of Clan Quest?
I was browsing the Runescape Forums for a clan, and once I read Clan Quest I thought, wow, that’s a pretty neat name.
Not some junk like Coven of Witches or Godless Heathens or something other overly edgy.
Hopped inside the Clan-chat as a guest and it was really nice and fun, well set-up, fantastic off-site as well.
Clan Quest just had a lot of effort put in, unlike any other Clan I’ve seen so far.
That’s what grabbed me, to be honest.
Coffee or tea?
Both.
Dirty Chai Latte is one of the best coffees I’ll ever drink.
Best thing of Clan Quest?
That its presentation is very well done.
As well as having monthly articles like this, very cool!
THE ALEX 43 SECTION BECAUSE WHY NOT
Did you find it yet?
I have found it!
Where was it?
Inside of my back pocket.
Are you going to take good care of it this time?
I’ll protect it with my life.
Do you have a new place for it?
No, it’ll go back inside my back pocket I’m afraid.
Is this place safe?
No, it keeps falling out at times.
Would it last a long time if it stayed there forgotten?
Not really, I’d sit on it too much, I think it’d bend eventually.
Do you need help?
I’ll ask a psychiatrist about that.
Is this a good idea?
Possibly?
Can you say that with confidence?
Possibly?
Is this how it's going to be?
Possibly?
BACK TO CHOTO
What is the meaning of life?
Everyone knows it’s 42.
Article by Xurdones
Table of Contracts
Hoods
My absolute favorite skill is Farming. A large reason is that the skill gives a lot of downtime. Time in which you can do a grinding skill. Farming gives you a break from that grind, while also being a relaxing grind itself. You can also pair it with another periodical skilling strategy, like birdhouses. I was level 83 Farming as of January 10, 2019, when the guild was finally released. It was the Spring semester of my sophomore year in college. In between studying or whatever assignments I was completing, I was on for 20 min doing a herb run every hour. I was doing the run before I left for class, and when I returned to the computer after class. I was quickly completing contracts to keep up with my dwindling seed stacks.
With the help of contracts in the Farming Guild, the Hespori, and the bottomless compost bucket, I was quickly approaching 99 Farming and finally got there on March 31, 2020.
Farming is easy, as long as you have the habit of doing a fast 20 min run every hour. That is the hardest part for most, making that a habit. Doing a run between Slayer tasks, or between trips to a boss. I will now describe the Guild in detail, in hopes you get the Farming fever like me.
The Farming Guild
The Farming Guild came with the Kebos Lowlands update on January 10, 2019. To enter, you must have the minimum requirements of 45 Farming and 60% Hosidius favor. To get there you must have started the Great Kourend questline to reach the continent. You may either run west from Lovakengj or use the fairy ring code CIR and run southwest.
There are many reasons why the Farming Guild is extremely beneficial:
- Completing Farming contracts yields more seeds, depending on the tier of the contract you complete. Higher level contract, higher level rewards
- Guildmaster Jane can trade your excess Spirit Seeds for a highest-level seed pack
- Anima patch affects all patches on Gielinor
- Your own Redwood Tree to chop down, no competition, but also no invisible boost you would get at the Woodcutting Guild.
- Hespori has a 1/35 chance to drop a Bottomless compost bucket that can hold all the compost you would ever need. All compost must be the same type. You can take compost straight from the bin with just this in your inventory. Also at a 1/16 chance, Hespori can drop White Lily seeds, grown in the flower patch, which protect all neighboring allotment patches from disease.
- The large compost bin gives 30 compost unlike the usual 15, and is especially useful for making ultracompost.
- The Seed Vault can hold all your seeds and saplings, saving bank space, although it is not available for Ultimate Ironman players.
- Pickpocketing Master Farmers without the bots elsewhere
- Bank booth and bank chest
- More Farming patches, more Farming experience
Four unique plants can only be grown here due to discoveries and the heat coming from Mount Karuulm:
- Celastrus - fletching the harvested product gives you battlestaves.
- Redwood Tree - cutting this tree once grown finishes an Elite Diary Task, but to uproot it you must pay 2k to Alexandra.
- Hespori, a Farming boss, always drops one of the three unique anima seeds every kill:
- Attas seed: increases the yield of Farming patches.
- Iasor seed: decreases the chance of Farming patches from becoming diseased.
- Kronos seed: provides a chance for Farming patches to skip a growth stage, effectively making them grow faster.
The Farming Guild is separated into three tiers, each requiring higher levels to enter. Each tier has a Leprechaun, a Master farmer, and water spouts or fountains for filling your watering can.
Level 45 Beginner Area
In the East you can find the patches for a Cactus, Berry, Flower, and two Allotments. A large compost bin that can hold 30 rather than 15 buckets of compost. Allotments, Bush, and Cactus can all be protected by Alan.
Level 65 Intermediate Area
In the West section, you can find patches for a Herb, Tree, and Anima. and the Hespori cave. Rosie may protect your tree and Arno at the entrance of the cave can retrieve your items if you die. You may also talk to Arno if you decide you would rather not receive Hespori seeds while farming. Felfiz Yaryus, a gnome near the Anima patch, can tell you more about the plants that can be grown there.
Hespori Boss: Lore and Farming
According to Arno, the Hespori is a rare carnivorous plant originating from Morytania, becoming conscious and highly aggressive once fully grown. They were also used as a weapon against Vampyres by Queen Efaritay. The Hespori's appearance is also extremely similar to that of The Maiden of Sugadinti, and it has been confirmed that there is a link between the two.
To randomly obtain Hespori seeds, you must check the health of fully grown trees, bushes or cacti, or from the last harvest of a regular plant such as herbs, hops, allotments, flowers, mushrooms, cacti, giant seaweed, or of course, from completing farming contracts. If you would like the option to not partake in the boss, you can speak to Arno, at the entrance, to stop randomly receiving Hespori seeds as you harvest, clear, or check the health of their crops around Gielinor.
Once 65 Farming, you can enter the cave and plant the seed. It is not necessary to water or compost a Hespori plant, nor does it need protection from disease. It takes 22-32 hours to grow, depending on when it was planted. The flower behind the cave entrance will be in bloom or open when the Hespori plant is fully grown. This way, you do not need to enter the cave to check if it is fully grown.
Killing the Hespori allows it to be harvested, which grants 12,600 (12,915 with full Farmer's outfit) Farming experience, as well as seeds, including the special drops: white lily, anima seeds, and the bottomless compost bucket.
Mechanics and Strategy
Francine’s Personal Best: 1:00.60, Compost Bucket kc 15
Four flower buds surround the Hespori. They all have 10 hitpoints, but will always die in one hit from any weapon. The Hespori is immune to damage while any flowers are open, and it will continue to attack while they are open.
They open up three times during the fight:
- once at the start of the fight,
- again after the Hespori goes below 66% of its health, and
- another final time after it goes below 33% of its health.
Hespori has three main attacks:
- A basic ranged attack that hits twice, both can hit 8 for a max of 16. It looks like Hespori throwing green spores.
- Protect from Missiles reduces the hits to a max of 2.
- A basic magic attack that hits up to 14, and looks like Earth Wave.
- With low Magic Defence, Protect from Magic is recommended though it will not entirely negate the damage, reducing it to a max of 3.
- An avoidable special attack that stops the player from moving and attacking every 50 seconds. Roots will entangle the players legs and the message: Hespori entangles you in some vines! appears in the chatbox.
- To avoid the damage of the attack, click to a new tile repeatedly to attempt to break free after 5 messages of: You feel the vines loosen slightly as you try to move. Attempting to move one last time will cause the player to break free. If the player does not break free after 10 ticks (6 seconds), it will deal 40+ damage.
Hespori is weak to slash, and attacks in both magic and range. So basic slash melee set up and Protect from Magic is the best option. Hespori is poisonous as well.
After entering the cave, drink a dose of combat potions and anti-poison, wield a ranged weapon, protect from magic, and “Harvest” Hespori to start the fight:
- Kill all four spores using ranged, turn Piety on, and switch to Special Attack with a Slash weapon, then keep slashing. Watch the chatbox for entanglement and eat when needed.
- Once 66% Health, turn Piety off, kill all four spores again using ranged, turn Piety on, and continue slashing the Hespori. Watch the chatbox for entanglement and eat when needed.
- Once 33% Health, repeat step 2, and special attack if you are able.
- Once dead, equip the Farming outfit, and “clear” Hespori for the rewards.
- Plant another Hespori seed and exit. The flower is now closed behind the cave entrance.
Note: At any point in the fight, you may leave the cave and re-enter to redo the kill. This can be done if you had a bad start, or were not ready.
I use a blowpipe for ranged, crystal halberd for slash special, and whip for a fast slash weapon.
Level 85 Advanced Area
In the North section, you can find four types of tree patches: Fruit, Spirit, Celastrus, and Redwood. There are also two bank booths, a center fountain, and a gazebo with a cat resting.
The Spirit Tree is protected by Gnome Latlink Fastbell
The Fruit Tree is protected by Nikkie
The Celastrus Tree is protected by Taylor for 8 Potato Cacti
The Redwood Tree is protected by Alexandra for 6 Dragonfruit and cut down for 2k gp.
Lobby
Guildmaster Jane
As her name implies, Guildmaster Jane is the head of the Farming Guild. She hands out Farming contracts for players to complete and gives a quick overview of the guild and its facilities. She can also trade spirit tree seeds for seed packs, which can be useful for players who have already grown the full spirit tree network and don’t see a reason in replanting them.
Farming Contracts & Seed Pack Reward
Farming contracts are a useful way to acquire seeds while training Farming. After asking Guildmaster Jane for a contract, the player is given a choice to choose a contract tier they’d like to complete, between easy, medium, and hard contracts. It is advised to always go for the highest tier available to the player, as they can always be downgraded later if needed. If your Hard contract is a seed you do not possess, you can then opt to get an easier one, a Medium contract, and if for the same reason, an easy one. Keep in mind, the harder the contract, the seed pack reward will offer a greater chance for higher-level seeds.
The optimal strategy for all tiers is to always have something growing in each patch that can receive a contract within the guild, of plants within the tier of contracts the player is attempting to complete.
For hard contracts, the basic strategy is as follows:
- Always have the following growing unless the contract says otherwise:
- Redwood tree
- Magic tree (because they take the longest to grow)
- Potato cactus
- Celastrus tree
- Watermelons (1 patch)
- Snape grass (1 patch)
- White lily
- Have any of the following planted, one in each category (shouldn’t matter which ones as the growth times are the same):
- Herbs
- Snapdragon
- Cadantine
- Lantadyme
- Dwarf weed
- Torstol
- Fruit trees
- Palm tree
- Dragonfruit tree
- Bushes
- Whiteberries
- Poison ivy
- Have maple and yew saplings (in addition to magic) ready in case a contract requests those
Always ask for a contract first, plant the requested plant, and then fill the other patches within the Farming Guild with the other ones listed. With any luck, the next contract will ask for one of the plants you’ve already planted, and you can complete it immediately. Continue until you get a contract you need to plant anew, then replant the checked plants.
While you can alternatively complete lower-tier contracts, they’re more difficult to complete in bulk because there are multiple possible plants for every patch. With hard contracts, you have roughly a 5/9 chance (55.5%) to get a contract you can complete immediately, while for medium the chance is 4/11 (36.4%) and for easy about 8/31 (25.8%). In light of this, it’s best not to think about optimising contracts until 85 Farming when hard contracts become available.
NOTE: Only plants grown within the Farming Guild count for contracts; there’s no reason to follow this guide for patches outside of it.
Seed Vault
The seed vault's primary usage is to reduce the amount of bank space used by seeds and saplings. Seeds or saplings stored in the vault are only accessible by interacting with the vault itself, so players may not want to store any Farming or tree run supplies within. The seed vault is ideally used for storing seeds and saplings that are not commonly needed, or for storing those that may be necessary for farming contracts.
The vault has a "Favourite Slots" tab where players can place up to eight types of seeds they frequently use, readily accessible for convenience. Similar to banks, it can also leave placeholders and it has a search function.
In addition, if players receive seeds from Managing Miscellania that are already present in the seed vault, they will automatically be transferred to the vault rather than the player's bank. For seeds that the player receives that aren't present in the vault, they will be placed in their bank instead.
The vault can not:
- Be used by Ultimate ironmen
- Store seeds or saplings given through quests.
- Store seedlings that have not grown into saplings.
I personally use the Vault to store all the seeds I do not use often, low-level and odd seeds for example. In doing so, if I don’t start my farm run at the guild, I still have the seeds I need.
Other Little Things
All things farming can be found in the guild, how convenient! The Garden Supplier for house plants, Allanna’s farming shop, and Amelia’s seed shop! No need to go to Falador Park for house plants, Olivia in Draynor Village, or the farming shops near other allotments!
Accessible to everyone, located in the lobby, is a bank chest, deposit box, and poll booth!
Found in crates and bookshelves around the guild, you can read the seven-book series “Gielinor's Flora” describing all the types of plants that can be harvested in Gielinor.
Unhoods
After getting 45 Farming and fast 60% favor in Hosidius, I hope to see you inside the guild! Fairy Ring code CIR! Make that 100% favor, so you can benefit from the disease-free allotment, flower, and herb patch in Hosidius! Favor is so fast! Just plough fields to 5%, make 850 sulfurous fertilizer to 90%, and complete The Depths of Despair for the last 10%!
For more information, refer to the OSRS wiki page.
I will be writing more Questaholic articles, so I would like to hear from you what Oldschool Runescape Content you are curious to learn more about. Please let me know, so then I can write another informative article that lets you know more about the other and oldschool side of Clan Quest.
For any other questions or inquiries, you may contact me on discord @Francine1225#2877
Until next time, unhoods
Article by Francine1225 and Diapolo10
The Clan Quest Test Kitchen
Hoods, and welcome back to Questaholic's Test Kitchen! This edition we're sliding away from the RS3 themed recipes to focus on something to warm the soul during this cold Winter. If you followed the Winter Warmer Cook Off then you'll already recognise this dish, and now you get the opportunity to make your very own delicious chicken and noodle soup! This recipe is rated at 2 out of 5 chicken legs if you're using store bought stock, 3 out of 5 if you're making your own stock.
Chicken Noodle Soup
Stock Ingredients
- 2 Chicken Drum Sticks
- 1 Large Carrot
- 1 Onion
- Chicken bones
- 2-3 Garlic Cloves
- Bay Leaves
- Black Peppercorns
- Thyme
- Rosemary
- Parsley
- Salt
- Pepper
Soup Ingredients
- Chicken stock
- 1 Carrot
- 1/2 an Onion
- 2 Celery Stalks
- Salt
- Pepper
- Egg noodles (as many "nests" as needed depending on serving size)
- Parsley (for garnish)
Before we start, let's talk Chicken stock. Chicken stock is the golden nectar of the gods that makes chicken soup just so tasty. If you're making the stock then I find you can keep the stock refrigerated for up to a week, or you can choose to freeze it for later use! Once you've made your chicken stock you'll be diluting it with water for the soup as pure chicken stock is pretty strong, and you don't need that much saltiness in your life. It's recommended you go 2 parts stock to 1 part water. Chicken stock is made with chicken bones, so the best time for making chicken stock is after a roast dinner or perhaps a bowl of chicken wings. The bones are only used for the stock, and can be disposed of after use.
- First we're preparing our vegetables for the stock. Now these don't need to be neatly chopped, and in fact do better in larger chunks as they'll be stewing for 90 minutes. Clean your veg, and roughly chop your carrot, onion, and celery into large chunks.
- The next step is surprisingly easy. Take all of your stock ingredients, and bung them in the pot. Simple! I recommend for the aromatics using 2 or 3 bay leaves depending on the size, a handful of black pepper corns, and whole sprigs of rosemary, parsley, and thyme. Presentation isn't important here as this is just the stock, but do mix everything up a bit within the pot.
- Pour hot water into your pot, enough to cover your ingredients, and bring to a boil. Once boiling reduce to a simmer. Place your chicken drum sticks into the pot to cook and add other flavours to the stock. I like to get the drum sticks with skin still attached as I feel that adds something extra to the broth. Adjust salt and pepper as needed.
- Now sit back and relax, as this bad boy will be gently simmering away for 90 minutes. You're going to want to keep an eye on the stock throughout this process though, adding more water if the water content drops too much, taste testing and readjusting salt and pepper, and skimming scum from the top of the stock. This isn't a particularly difficult process, just a long one.
- After 90 minutes you should be left with a golden liquid amongst the ingredients. That's your stock! Using a sieve, strain your stock into another pot or container to separate the solids from the liquid. Remove the chicken drum sticks from the solids and set aside, as we'll be using them for the chicken and noodle soup. All other solids can be disposed of after this point.
- Behold, your stock! Delicious, tasty, chicken stock. At this point you can either refrigerate/freeze for later use, or you can start cooking your chicken and noodle soup.
- Taking your chicken drum sticks, pull the meat away from the bone. This shouldn't be difficult as after stewing for 90 minutes the meat will be practically falling off. Using a couple of forks, shred your chicken into smaller pieces. Set aside for later use. If you didn't make your own chicken stock then you'll need to cook a chicken breast in addition to your chicken and noodle soup ingredients for this purpose.
- Prepare your veg by cutting into smaller pieces (whichever size you'd prefer for your soup), and set aside as well.
- Using the ratio of 2 parts stock to 1 part water, fill your pan with your preferred amount of broth. This will be dependent on how many servings you are making. Get the stock going on a medium heat, then add your shredded chicken and vegetables. Cook this for 15 minutes, taste testing and adjusting salt and pepper as necessary.
- Finally, your egg noodles. Depending on if you're using fresh or dried the cooking times will be different, and I encourage you to follow the manufacturer's instructions. Normally serving size will be represented as one nest per person. Add as many nests as you need to the soup.
- After a total cooking time of 15 minutes, your soup should be ready! You may wish to pour in the soup broth first and then add the solid components of the soup to avoid mostly broth. Serve your soup with a parsley garnish for aesthetic. And voila! You have made chicken and noodle soup!
I really enjoyed making this soup during the cook off, and definitely enjoyed eating it. As it's getting colder it's nice to have foods like this you can to some extent prepare ahead of time to enjoy. I hope you enjoyed making this dish as much as I did!
This brings us to the end of this years Clan Quest Test Kitchen! It's been a pleasure cooking with you these past editions, and I hope you've learnt something from this experience. I definitely learnt a lot! I'll see you all for now, and wish you a Happy Holiday season and a Happy New Year! Unshood for now folks!
Article by Darkestnight
The... Christmas Tree variation?
The subject of this article will be a specific chess opening; as such, I cannot avoid using chess notation to write down the moves that are played. If you are unfamiliar with chess notation but are still interested in this guide, I advise you to take a quick scroll through JoeTribiani's guide on chess notation.
Yes, you read that correctly! This edition of Questaholic will be the first edition in which I discuss a chess opening. With a merry holiday spirit in mind, I went looking around the far reaches of the internet for a holiday-themed opening. My eyes stumbled upon a variation of the Dutch Defence (which, as a Dutchie, I'm obligated to be partial to) known as the Christmas Tree variation.
In chess, openings are given certain names for a multitude of different reasons. Sometimes, the name is determined by the way white sets up their pieces, and other times, the most important is the way black sets up their pieces. The Dutch Defence is an example of the latter; a chess game enters the Dutch Defence typically through the opening moves 1. d4 f5. This opening is a cousin of the more well-known Sicilian Defence, which we can arrive at through the opening moves 1. e4 c5; an astute observer might realise these openings are the mirror image of each other. Now, usually when someone plays the Dutch Defence, they have a particular system in mind. These systems often include a pawn on e6 (which is known as the classical Dutch) or a pawn on g6 (the Leningrad Dutch). The Christmas Tree variation is a combination of these systems, in which black pushes both his e-pawn to e6 and his g-pawn to g6. Black's pawn structure now contains what we would usually refer to as a triangle, but in this particular case, we instead view it as a Christmas tree! More visually, a typical position in the Christmas Tree variation would look like this:
Now, I did not simply make this position up; it has been reached many times in online and over-the-board play. Just scrolling through Lichess' games database, I can find the above position (or similar) in games by many strong players, such as Anton Korobov, Gabriel Sargissian and Simon Williams. You can check out the following reference game played at a classical tournament in Mumbai in 2020, between Uzbek Grandmaster Nodirbek Yakubboev and Indian Grandmaster Sandipan Chanda. These are two incredibly strong players. Yakubboev, at only 20 years old, is currently the fourth highest-rated player from Uzbekistan. He played for the Uzbek team at the last Chess Olympiad in Chennai, India. By average rating, the Uzbek team were the 14th strongest, but they actually managed to win the tournament! Yakubboev even won an individual bronze medal for his second-board performance. His opponent in our reference game, Sandipan Chanda, has played on the Indian team for multiple Chess Olympiads, was Viswanathan Anand's second for the latter's world championship match in 2013, and has even won the Open Dutch Chess Championship twice (in 2016 and 2017).
At 39 years old, Sandipan is definitely the more experienced player of the two. In this game, he (successfully!) employed a strategy that you see very often when an older player faces a talented youngster. Talented youngsters are usually very well prepared in standard opening lines, with tons of engine-assisted preparation in their toolbox. Therefore, their older and more experienced opponent typically takes the game into an offbeat opening line very early on, in which the youngster's opening preparation is useless and the older player's chess experience gets more opportunity to shine.
For those who would like more information on this opening, I will point you towards a particular YouTube video by the (previously mentioned) British Grandmaster Simon Williams, better known online as GingerGM. In this video, he talks about the Christmas Tree variation and includes analysis about a game he himself won, in which he played our beloved Christmas Tree variation. An interesting difference between our reference game and the Simon Williams game, is the center pawn break black used on their road to victory. In the video below, Williams talks about how he wants to prepare and play the pawn break on e5, whereas Sandipan played for a pawn break on d5.
Other chess news
- American Grandmaster Hikaru Nakamura has won the online Speed Chess Championship for the fifth time in a row! This was an incredible tournament to watch, with the crème de la crème of the world in terms of speed chess competing in a knock-out tournament for the title of Speed Chess Champion. The final match was between Nakamura and current World Chess Champion Magnus Carlsen, and it was perhaps an even more exciting match than the final game of the 2022 football World Cup (which was coincidentally held on the same day). For a 30-minute recap of the match, I will direct you to this video.
- Depending on when this edition of Questaholic is published, this year's World Rapid and Blitz Championships might be ongoing! They will be/are/were held between December 25 and December 30, in the city of Almaty, Kazakhstan. Many strong chess players from around the world will gather in Almaty for three days of rapid chess to determine who, if anyone, will succeed the Uzbek youngster Nodirbek Abdusattorov as World Rapid Champion, followed by two days of blitz chess featuring the same title defence efforts from French Grandmaster Maxime Vachier-Lagrave.
- From January 13 to January 29, the Tata Steel 2023 tournament will be played in Wijk aan Zee, a coastal village in The Netherlands. Despite its seemingly unimpressive location, this tournament is an absolute staple in the annals of top-level chess, and this year's master section line-up is perhaps the strongest it has ever been. It includes the reigning World (and Tata Steel) Champion Magnus Carlsen, who will be joined by a cast of established top players, as well as a number of extremely talented youngsters from all over the world. As a Dutchie, I might be a little biased, but this is as exciting as a tournament can possibly get.
- The dates for the next official Chess World Championship match have been announced! The match between our top two finishers at the last Candidates tournament, Ian Nepomniachtchi and Ding Liren, will be played from April 7 to April 30, 2023. This will be a match for the history books, as it will be the first match in which the reigning World Champion does not defend his title (since Alexander Alekhine's death in 1946). As far as I'm aware, FIDE has not yet announced the location of the match.
Article by Derparnieux
Shiro Applies Maths: Music theory - The final note
Welcome everyone to the final part of Music Theory. I've proudly worked on this piece at my university and I'm happy that I'm able to share this with you. We've got a full schedule today, so I'll keep the introduction short. I hope you'll have a merry Christmas and a happy New Year! You know the drill by now, take a cup of hot choco and enjoy!
Equal Temperament
In the mid-nineteenth century, it became more important for large ensembles to play together in a bright variety of keys. Equal temperament was what made this possible and is explained further in this article. Simon Stevin was already a supporter of equal temperament in the sixteenth century. We will start with a short biography of Stevin. His 'proof' that equal temperament represented the true pure ratios will be given later in this issue.
Simon Stevin
Simon Stevin (1548 - 1620) enrolled at Leiden University when he was 35 years old. This is where he met Maurits (Maurice) of Nassau, prince of Orange. Stevin would end up tutoring Maurits on several subjects, such as mathematics and science. In order to do so, he wrote several educational books for Maurits, but in spite of the educational aim he always added something, or even much, of his own to these works. The oeuvre Stevin produced in his lifetime is nothing less than extensive. As a fervent lover of the Dutch language, most of his works are published in this language. Stevin also tried, whenever he could, to implement an equivalent Dutch word instead of the term that was used everywhere else. He introduced the concept of decimal fractions and showed that the ease of operations on them was comparable to that of integers. Besides this, he was opinionated that all numbers - including squares, square roots, and negative or irrational quantities - were of the same nature. This means that he found that √2 is not more special or complicated than the number 2. Initially, this was unaccepted by the mathematical community, but as time passed mathematicians became used to the idea and eventually used them for algebraic purposes. Stevin also introduced different proof methods and deviated in this from the Greeks who proved by reductio ad absurdum. The view Stevin has on numbers, was also used in his idea on the theory of musical tuning. He believed that the pure octave, the perfect fifth and the pure third should all be combined in an equally distributed scale. In doing this, he deviated from all commonly used ratios, except the octave. As he did not believe that, for example, 2:3 is more perfect than any other ratio.
Equal Temperament
To understand the definition of equal temperament, we first look at the Oxford English Dictionary that defines it as:
[Temperament] (now almost universal), in which the octave is divided into twelve (theoretically) equal semitones, so that the variations of pitch are evenly distributed throughout all keys.
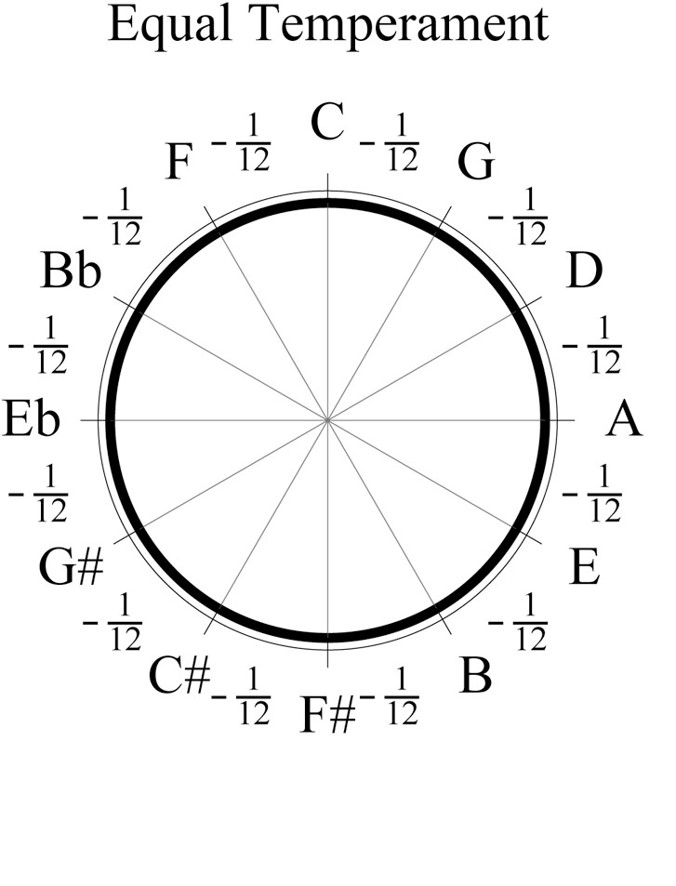
This means that an octave is divided into twelve equal steps, each step being of length ¹²√2. In the systems before equal temperament, the division of an octave depended on the preferred choice of ratio, albeit 3:2 in Pythagorean tuning, 5:4 in ¼ comma meantone temperament, or something else entirely. Equal temperament only kept the octave (2:1) as perfect ratio, all other ratios had slight alterations. These deviations lead to greater flexibility in musical ensembles with a multitude of instruments. Because of the equality, instruments in different keys can easily play together. This was an improvement, as before only a musician with freedom to choose their own pitch, such as vocalists or violinists, could easily adapt to musicians restricted to fixed temperaments. Besides the advantages for musicians, it solved the appearance of the wolf-whistle in the circle of fifths. As all step sizes are equal, it is evident that raising a fifth (¹²√2⁷, as shown in the Figure below 12 times, result in a pitch seven octaves higher than the initial, as (¹²√2⁷)¹² = 2⁷. Initially, equal temperament was not commonly accepted, as there was no necessity for this wider variety of music. Society also valued perfect ratios more highly than a wider range of musicality. In accepting equal temperament, Stevin mostly agreed with the theories of Vincenzo Galilei, the main founder of equal temperament as we now know it. However, he disagreed with the necessity of keeping the perfect fifth as an integer ratio, but opinionated that a 2:1 ratio should be divided as twelve times ¹²√2. In the modern musical community, these aberrations are only recognized by people with extremely sensitive hearing. In modern western music, the advantages of ease of transposition weight above those of perfect ratios.
In Stevin's unpublished manuscript Spiegheling der Singconst, the concept of dividing a string into perfect ratios, for which a monochord is used, often appears. It is quite natural to divide a string into two equal parts, the sound that is then produced is similar to that of the undivided string. Dividing this half of the string into two or three parts is still a natural process. If we assume a string to be 144 parts long, this iterative division then results in:
These places are indicated on the fretboard and produce 'pleasant sounds' which are denoted by the corresponding letters as suggested in the introduction to 'Simon Stevin's View on Music'. Note here that A, a, a' are numerically represented by 144, 72, 36, all of which are in the ratio 2:1, which is exactly what equal temperament is supposed to do.
As Stevin was a practised lutist, it makes perfect sense that he was interested in equal temperament. A lute is a fretted instrument which requires a different tuning, as the distance between frets is predetermined. As a mathematician, it makes sense that he wanted to create a mathematically sound system for these instruments. What characterized Stevin's work, and distinguishes it from others, is that he tried to prove that the octave can be divided into twelve equal steps. He aspired to do this in two steps; first he wanted to show that the octave comprises 6 equal whole tones and then show the existence of 12 equal semitones in one whole octave.
Stevin's Proof
To prove his postulate as given below, Stevin first defined a few concepts, followed by his postulate. The most important one being:
Two sounds having the same pitch. The relation between two such notes is called 'first' or 'prime'. When they differ by one step it is called 'second', with the prefix 'major' or 'minor' to indicate the specific relation if relevant. Five major steps and two minor steps together form an octave.
Postulate: All whole tones should be equal, likewise all semitones should be equal.
This postulate is followed by a somewhat weird explanation as 'proof'. Stevin assumes that there are two harpsichords X and Y with the properties that the B tone on X is equal to the F tone on Y. Then the interval F(X) (F played on instrument X) - B(X) (B played on instrument X) consists of three tones, as it is an augmented fourth. The interval F(Y) - B(Y) also consists of three tones. Stevin then argues that experience shows that F(X) - B(Y) is indeed an octave and this proved the proposition, or so Stevin thought. In equally tempered instruments this is indeed true, since F(X) - B(X) as a three tone, implies that B(X) - F(X) consists of a two whole toned and two semitoned interval. Per definition of an octave, this interval is also called the diminished fifth. Then, as B(X) = F(Y), F(X) is four tones higher than B(X), and B(Y) is three tones higher than F(Y), it is clear that F(X) is 3w + 2w + 2h = 6w = 1 octave higher than B(Y). However, in mean tone temperament this equality does not follow, as a whole tone in mean tone is of size √⅘ and when we raise this six (five whole tones and two semitones) times, it does not result in a perfect octave as (√⅘)⁶ = ⁶⁴⁄₁₂₅ which is not equal to ½. This deviation from the perfect octave is quite considerable. Had Stevin tried performing his idea or proof on two harpsichords that were tempered in mean tone, he would have heard this. As a similar example is given for the second part of the proof, with the same faults, it would suggest one of two things, either Stevin had terrible hearing, or he simply did not try this on instruments that were not equally tempered.
It is almost as if Stevin anticipated his blunders, as he dedicates a whole chapter in the appendix to the Cause of the Imperfection that Arises when Organs and Harpsichords are Tuned. This chapter explains, by using a metaphor, that it is impossible to tune instruments perfectly. The differences between pure and applied mathematics, would be so extensive that they will always be recognized in the real world. In writing this, Stevin forestalls his above-mentioned faults. However, these imperfections in tuning would still result in relatively similar tones, thus it does not explain why Stevin argued his example to be true. A more appropriate explanation would be that Stevin is a-musical, as suggested by Cohen in his explanation on this subject. As Stevin started developing his theory to incorporate it on other instruments than the lute, he had not yet realised that his lute was in fact equally tempered. When this information is combined with the fact that he did not hear the differences between perfect ratios and those that are not-so-slightly off, it would make sense to say that Stevin was just not musically skilled. The whole development and arguments in his treatise hinge together on his opinion that the pure ratios are not integer ratios, but rather the ones fabricated by equal temperament. However, the results of this equality are used in the contemporary music industry.
Circle of Fifths
As the octave is divided into twelve equal parts, all parts have value ¹²√2. Starting at a note C and raising this with a fifth, result in a note G of value ¹²√2⁷. To complete the circle, a C is raised by a fifth twelve times to get a new C. This C now has value (¹²√2⁷)¹² = 2⁷, which is precisely seven octaves higher than the original. As a result, the circle is completed without a wolf-whistle. This circle is depicted in the figure below.
Christiaan Huygens
Last time I promised you not one but two Dutch mathematicians. We've just covered Stevin and we will now delve a bit deeper into Christiaan Huygens and his 31-tone temperament.
Christiaan Huygens (1629 - 1695) followed in the footsteps of Simon Stevin to Leiden University at the age of sixteen, where he would study Mathematics and Law. Afterwards he continued studying Law at Collegium Arausiacum in Breda. He would become most known for the high positions he acquired in several fields and his discovery of the ring of Saturn, the invention of a pendulum clock and his theories on light. When he was only eight years old, Huygens's father deemed it necessary to teach him the art of singing. Huygens turned out to be a very proficient in the art of all things musical, it be vocalizing, playing the violin, the lute, or a harpsichord. Until age sixteen he was educated at home by several private teachers and his father, learning several languages and sciences. During his mathematical studies, Huygens was greatly influenced by Descartes' works. This is unsurprising, as Descartes visited the family's home and often corresponded with Huygens' father. His father had an extensive study collection, amongst which was the manuscript Spiegheling der Singconst from Stevin, which could suggest that this work affected Huygens. Even after he went to University, he remained very interested in music theory and especially in the problems with tuning and temperament.
31-Tone Temperament
The definition of a 31-tone equal temperament is similar to that of a 12-tone equal temperament and only noted by the interpretation of a musical scale. In 12-tone temperament, as the name suggests, a scale is divided into twelve equal parts. A 31-tone temperament is thus based on the division of an octave into 31 equal parts. This conceptual idea bases itself on the perfect intervals and the unwillingness to compromise in their perfectness. When an octave is equally divided into 31 parts, there is a significant improvement in the ratios compared to meantone temperament. Besides this, in using the equality, it prevents the occurrence of a wolf whistle in a circle of fifths. Huygens name has been connected to this system for a long time past. This tonal system has thus also been called the Huygens System.
Huygens is definitely not the first to attempt to create a 31-tone scale. Salinas and Mersenne, both sixteen century mathematicians with a love for music, tried this idea in their days, however quickly disregarded it, as they experienced that tuning by the 31 tone system proved to have bad results for the ears. As Huygens continued developing this idea, he acknowledges the struggles that both these men could have experienced and proposes a solution, which will be explained after this. The idea behind equal temperament, as Stevin proposed in his work, had probably been read by Huygens. In a synopsis of his manuscript, he mentions a chapter Contre Stevin, which means against Stevin. Huygens despises the idea Stevin proposes, as none of the perfect intervals are kept pure or remotely similar. He also agitates against Stevin's lack of musical knowledge. However, the concept of equal division of an octave is something he accepted.
Huygen's letter
(Disclaimer, We're going to do some calculations with logarithms. Since wiki is a bit difficult with notation I'm going to say now that all logarithms in this article are of base 10. Also don't worry, I've done the calculations for you).
Henri Basnage de Beauval, editor of the journal Histoire des Ouvrages des Scavans received a letter from Huygens concerning his view on the 31-tone temperament and his 'proofs' that this temperament was not to be disregarded as his predecessors did. Huygens argues that this system is superior to all prior systems. He concludes that the 31-toned perfect fifth, and consequently also the perfect fourth, did not differ from the regular temperament by more than ¹⁄₁₁₀th of a comma. This resulted in a difference to the just perfect fifth by ¼-¹⁄₁₁₀ of a comma. He argues that this difference is unperceivable by the human ear, and would thus have little difference to the regular temperament. Compared to regular temperament, the major third exceeds the perfect interval by ⁴⁄₁₁₀ which is approximately ¹⁄₂₈ of a comma (Huygens uses an approximation here, it is unclear why this is done as it was not necessary). He argues that this difference is minor and can thus be endured easily, as the people had endured ¼ of a comma (in the perfect fifth) before. However, this impedes the reasons for using regular temperament, as that was created to alleviate the stress on major thirds, since they were deemed more important than perfect fifths when playing chords. In saying this, Huygens argues that ¼ comma difference in a third is on par with a ¼ comma difference in a perfect fifth. This is certainly not the case. Finally, Huygens concludes that the minor thirds are smaller by ³⁄₁₁₀ which approximates ¹⁄₃₇ of a comma than the regular temperament and consequently the major sixths are larger by ¹⁄₃₇ of a comma. He again argues that ¹⁄₃₇ of a comma cannot be perceptible, nor noticeably augment the ¼ comma that these consonances already are away from the true ratio in this temperament.
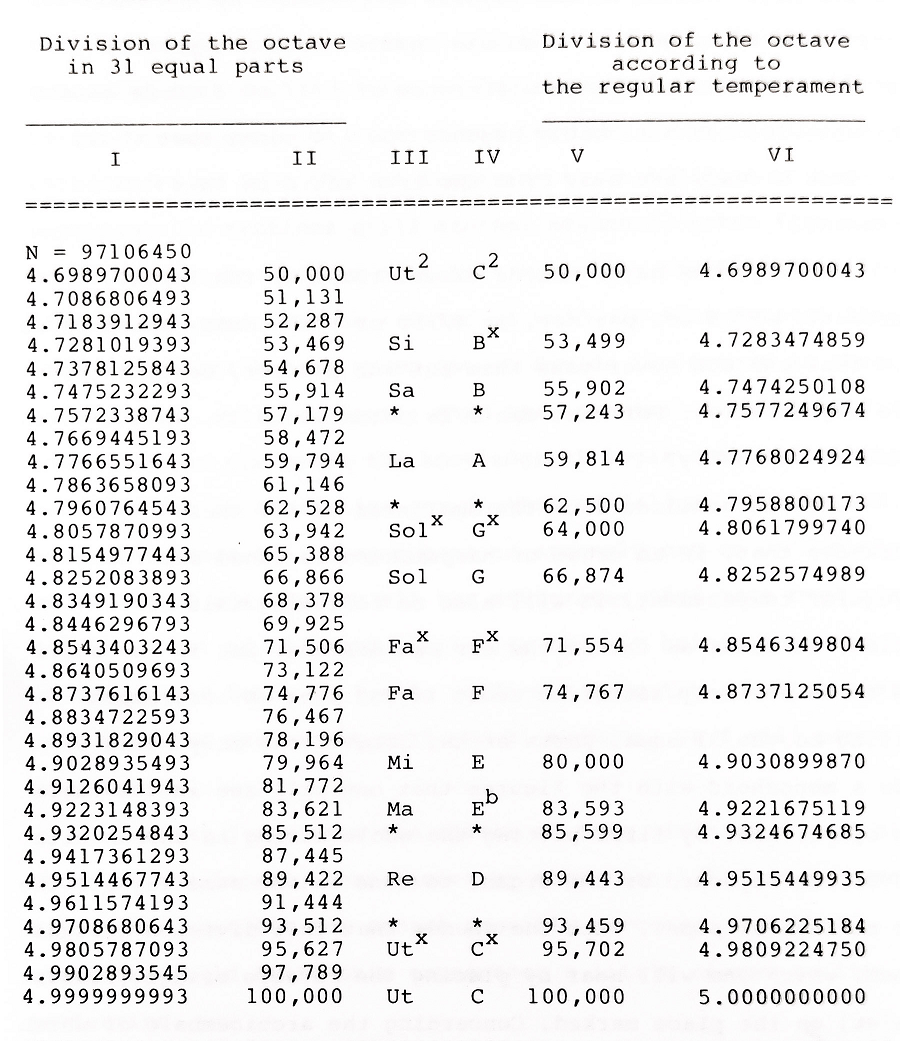
As mentioned before, Huygens gives an argument as to why people like Mersenne and Salinas failed at making the 31-tone temperament work. This argument is that the use of logarithms is necessary, a mathematical concept not available during their research. In his letter, Huygens added a table to use in his calculations, as shown in the Figure below. This table consists of six columns and can be divided into two parts. The first two columns show a new system to calculate string length, the final two columns indicate how this was done before, column III and IV demonstrate the corresponding pitchnames. In his system, Huygens starts with a string of length 100,000 that has pitch C. Since an octave has ratio 2:1, a string of 50,000 parts would then be c². He then calculated the log value of this length, which is log(50,000) approx. 4,6989700043. In order to find the logarithmic values of all other tones, Huygens calculated each increase as
N = ¹⁄₃₁log(2) which is approximately 0,0097106450.
This value is similar to that of ¹²√2 in 12-tone equal temperament. Then by simply adding this to the previous value, he obtained the desired first column in the table. The last value that corresponds to a length of 100,000 parts is equal to 4,9999999993 approx. 5.0. The second column shows the corresponding string lengths of the 31-tone temperament. This value is obtained by raising ten to the power of the corresponding value in column I. A word of caution is necessary, as it is unclear in what order Huygens did these calculations. The fifth column contains the already known string lengths of the regular temperament, with the sixth column containing their corresponding logarithmic values.
Huygens gives an example to show how to use this table to calculate the distance of each interval. This example goes as follows. Suppose that one wants to check whether the fifth C-G of the regular temperament is ¹⁄4 comma less than the perfect fifth, which has ratio 3:2. In the previous article it is already determined that the whole comma has a ratio of 81:80. Its logarithmic distance is then equal to log(81)-log(80) = 0,0053950319. Consequently, ¼ of a comma is then 0,0013487580. The next step is to check whether the difference in size between a perfect fifth and the regular temperament's fifth is equal to this ¼ comma. In the sixth column, we find the logarithmic value of C and G, which are respectively 5,0 and 4,8252574989. The difference between these values is 5,0 - 4,8252574989 = 0,1747425011. This then represents the size of the fifth in regular temperament. The ratio of the perfect fifth is 3:2, so its size is equal to log(3)-\log(2) = 0,1760912594. The size of the perfect fifth is larger than the regular's, meaning that the regular fifth is flatter than the perfect fifth. The difference between the two is then equal to 0,1760912594-0,1747425011 = 0,0013487583. This is approximately equal to the earlier determined ¼ comma. Therefore, it is shown that the regular temperament is ¼ comma less than the perfect fifth.
Huygens then proved that a fifth in the 31-tone temperament is ¼-¹⁄₁₁₀ comma less than a perfect fifth. Let a fifth for example be D-A. In the first column we can then find the logarithmic values for D and A. The difference between the two is then equal to 4,9514467743 - 4,7766551643 = 0,1747916100. This value is indeed smaller than the perfect fifth, meaning that it is flatter than the perfect fifth. In order to determine by how much we subtract this value from the perfect fifth's value, obtaining 0,1760912594 - 0,1747916100 = 0,0012996494. This is smaller than the ¼ comma by a margin of 0,0000491086. The final step is to divide this margin by the value of the whole comma, which is 0,0053950319. This gives a value very close to ¹⁄₁₁₀. Meaning that a fifth in Huygens' new division indeed differs ¼-¹⁄₁₁₀ comma from the true fifth.
Huygens felt it was too much work to include the calculations for all other intervals and ended his letter. He often says the calculations with logarithms are easy to perform and for that reason we're going to do one more calculation to confirm his conclusion. In this calculation we're going to check his conclusion on the major third, say C-E. Huygens claimed it approximately differed with the pure major third by ⁴⁄₁₁₀ comma. A pure major third has a ratio of 5:4 and thus its size is equal to log(5)-log(4) approx. 0,096910013. This value can also be obtained by taking the difference between the logarithmic values of C and E given in column VI. Similarly we can obtain the size of the major third by taking the difference between the C and E from the first column, resulting in 4,9999999993-4,9028935493 approx. 0,09710645. The 31-tone major third is thus marginally sharper than the pure major third as its size is larger. This margin can be obtained by taking the difference between the two, which is 0.000196437. This divided by the size of the whole comma indeed gives (approximately) ⁴⁄₁₁₀, meaning that Huygens conclusion about the major third differing by ⁴⁄₁₁₀ is correct.
Circle of Fifths
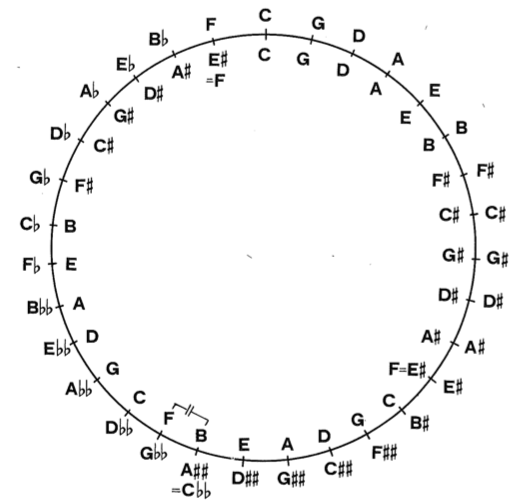
Of course we need to end on another Circle of Fifths.
The cicle of fifths for 31-tone equal temperament is akin to that of the 12-tone equal temperament. The Figure below shows this circle for the 31-tone on the outer layer, compared to a repeated 12-tone circle. As equal temperament is defined around the pure octave 2:1, it obviously true that this circle then again converges.
You guys are heroes
For anyone who has come to this part, kudos to you because this has been a long ride. I admit that this article was not an easy read, but nonetheless I believe this was interesting to read. I've spend five weeks on the complete paper and I enjoyed it very much. Thank you all for allowing me to share this with you guys. The bad side of this is: I need to find a new topic to write about and boy did I set the bar high. I hope you all have a merry Christmas and see you next year on Shiro Applies Maths.
Article by Shiro Shana
Followers of my work won't be surprised to hear that I really, really, really enjoyed Knives Out, the 2019 mystery/comedy written and directed by Rian Johnson; it was a delightful viewing experience, a well-executed fair-play whodunnit that nevertheless was able to subvert the formula in ways that were novel and surprising. If you haven't seen it yet, I heartily encourage it. So I was understandably exited for the sequel; cautiously excited, because sequels to brilliant original premises are often disappointing, but excited nonetheless.
Once I started watching Glass Onion, that excitement...did not last. Oh well.
Let's start with the basics. The premise of the film is that eccentric tech billionaire Miles Bron (Edward Norton) is throwing a murder mystery party for his friends at his Greek island estate. The attendees, and our main cast, are: supermodel-turned-fashion-mogule Birdie Jay (Kate Hudson), and her belaguered assistant Peg (Jessica Henwick); Men's Rights Activist Youtube Twitch personality Duke Cody (Dave Bautista), and his arm candy girlfriend Whiskey (Madelyn Cline); corporate scientist Lionel Toussaint (Leslie Odom Jr.); and Claire Debella (Kathryn Hahn), the Governor of Connecticut. Also along for the ride, to the great surprise of everyone, are Cassandra "Andi" Brand (Janelle Monáe), a former friend and business partner who recently lost a very high-profile lawsuit claiming partial ownership of Miles' company, and Benoit Blanc (Daniel Craig), world-famous master detective and the only returning character from the first film. As the entourage arrive at the island and Blanc gets to know them all, two things become very apparent.
Firstly, every person there (with the lone exception of Whiskey) have very good reason to want Miles dead: Andi for cutting her out of their company and leaving her with nothing; Birdie and Peg because Miles is setting Birdie up to take the fall for the use of sweatshop labour by their shared clothing company; Lionel and Claire because Miles is pushing forward with an untested and potentially dangerous new project, which Lionel developed and Claire pushed to legalize; and Duke because he discovers that Whiskey is cheating on him with Miles.
Secondly, Blanc was not actually invited; the invitation he received having been forwarded to him by one of the other guests. Miles believes this is someone playing a joke (imagine inviting the world's greatest detective to play your murder mystery game), but Blanc is concerned that, given the last paragraph (and his experience in the previous film), this means somebody might intend to actually murder Miles.
And with that, the game is afoot.
Explaining much more of the plot will get heavily into spoiler territory - it is a murder mystery after all - so I'll save the details for later. For now, suffice to say that a murder occurs, Blanc is enlisted to solve it, and shenangians ensue.
I tipped my hand a bit at the start of this article, and the truth is that I didn't particularly like Glass Onion; it was an enjoyable enough film, but "merely enjoyable" is a major disappointment compared to its predecessor, which quickly became one of my favourite films, and there are enough flaws in the execution that let the experience down quite significantly. But I think I'm ultimately going to say some very unkind things, so let's soften the blow by starting with the positive elements.
For starters, the film is visually beautiful. The mansion set, home of the titular "glass onion" central structure, is magnificent, and there's tremendous use of lighting throughout; most noticeable is shortly after the murder, when - as a pre-arranged part of Miles' game, turned tragic by unforseen circumstances - all of the interior lights go out, and the characters are lit by nothing more than the rotating beam of the lighthouse. It's a visually-striking scene, unlike anything that I've seen in a film before (and there's an interesting Twitter thread by the film's Director of Photography explaining how they accomplished the effect).
For another, the film makes great use of its editing to mislead the audience, and this is where mentioning spoilers is unavoidable. The first notable occurrence is immediately after the murder of Duke, who suffocates despite nothing blocking his airways. Miles, who has been primed by Blanc to expect an attempt on his life, very quickly notices that Duke had drunk from Miles' glass, not his own (Miles had supplied all of the party guests with monogrammed glasses for their drinks), and assumes that someone had poisoned it, and Duke had picked it up by accident when the two men sat next to each other; the film even shows us a flashback scene of exactly this happening. The problem is, as Blanc points out later (and is confirmed on a re-watch), that isn't what happened: Miles handed Duke the glass as he sat down, which is one of the clues that Miles is actually the murderer and not the victim. The misdirection works because audiences expect flashbacks to be accurate, but is fair because an attentive viewer will have seen the the truth slightly earlier.
The second example is one that makes use of the "negative space" between cuts. See, the audience is shown three scenes of the guests receiving their invitations, which take the form of a large box full of puzzles, which need to be solved before the invitation card is revealed: the first is a split-screen scene of Birdie, Claire, Lionel, and Duke receiving their boxes and solving together on a group call; the second is Andi receiving her box and smashing it open with a hammer; the third is Blanc playing Among Us with his friends over Zoom, and the off-screen voice of his roommate/boyfriend (it's ambiguous in the film but confirmed in interviews that Blanc is gay, and the voice is his partner) saying that a box arrived for him; then we cut straight to the characters waiting for the ferry to take them to Miles' island. We never actually see Blanc receive the box, and the audience assumes that it's a time-saving cut; we've seen the puzzles be solved, and Andi smashing the box reveals something of her character, but we already know Blanc, so showing either again would be unnecessary. The twist, which is revealed halfway through, is that we never saw Blanc receive a box because Blanc never received a box at all; he was "invited" by Andi, who showed up at his apartment with her own, smashed-open box, and enlisted him to help pull a con on Miles and the others.
That said, while technically interesting this second example gets to the heart of what I disliked about the film: this reveal isn't fair. In fact nothing about the film is fair, it withholds vital information until well into the second act, not only making the mystery impossible to solve until nearly the moment Blanc solves it for us, on-camera, but intentionally obscuring what the mystery even is. For example, remember how I said a moment ago that Blanc was invited by Andi? That was a lie. Andi has been dead since before the movie began, and solving her murder is the actual central mystery of the film. The character we meet as Andi is actually Helen, Andi's identical twin sister. She found the box among her sister's personal effects, suspected one of Miles' entourage of murdering her, and hired Blanc to infiltrate the party and identify who it was. This is the actual core premise of the film, and we don't find this out until an hour and a half into a two-and-a-half hour film.
I understand the intent, as with all twists the intent is to surprise the audience; plus, the first film is notable for (among other things) using information the audience wasn't privvy to in order to re-contextualize the scenario. The problem is one of information asymmetry: in the first film, the audience had access to the same information as the viewpoint character; it was okay that certain things were revealed to us later, because they were being revealed to her at the same time. Glass Onion violates this because our viewpoint character is Benoit Blanc, but he has vital information the audience lacks. The consequence is that the first half is basically entirely pointless: there's significant time spent on the fractured relationship between Andi and the other characters, but none of that matters because that isn't actually Andi, and both she and Blanc know this; likewise there's a lot of tension built up about who is going to kill Miles, but Blanc knows that nobody is planning to kill Miles.
Finally, and most annoyingly, it means that all of the motives everyone has to kill Miles are also pointless tension, because nobody wants to kill Miles. This is best exemplified by a scene where Duke, with Blanc following at a shrot distance, appears to randomly stumble past Miles' bedroom window while he and Whiskey are having sex; a scene of Duke tightening a fist emphasizes his frustration and anger, and the audience is led to believe the discovery of the affair is the cause. But we revisit this scene later on, and see that there were bits cut out: specifically a conversation earlier, overheard by Helen, where Duke convinces Whiskey to sleep with Miles and convince him to give Duke a coveted timeslot on one of Miles' TV networks, and then while Duke is watching the affair we now learn that he can overhear them talking, and his frustration is directed at Miles' unwillingness to give him the slot. He has no motive to kill Miles, Blanc knew this, but the film lies to the audience to preserve the first-act mystery.
Some time ago I listened to a podcast review of Star Wars: The Last Jedi, which was also written and directed by Rian Johnson; I generally liked that film, but one of the criticisms on this podcast that I agreed with was that the only really clever things he did were straight inversions of audience expectations; there was no clever twist, it was just "this thing that usually happens in other Star Wars movies instead does the complete opposite", and that kind of writing is no more creative than just leaning into existing tropes and stereotypes. I feel similarly about Glass Onion: it's a basically-fine movie that wants to be as clever as its predecessor, but fails because the only thing it knows how to do is flip the script.
Article by Xurdones